目标：

1. Monte-Carlo的来源
2. 意义
3. 应用
4. 可视化

概念

蒙特卡洛方法是一类计算方法的统称，依靠重复采样的方法来获得数值结果。它的核心概念是用随机性来解决一些确定性问题。事实上，蒙特卡洛方法没有一个很清晰的定义，不同领域的不同学者有着各式各样的解释。一个经典的例子是使用随机落针的方式来估算$\pi$的数值。

应用

在RL中，蒙特卡洛搜索树可以用来估计值函数。从一个节点出发根据策略模型随机采样动作，而后模拟一整轮游戏以获得奖励。多次模拟后，经验奖励的平均就可以用来更新节点的值函数，评价节点状态的好坏。

可视化示例

1. 估算pi值
   
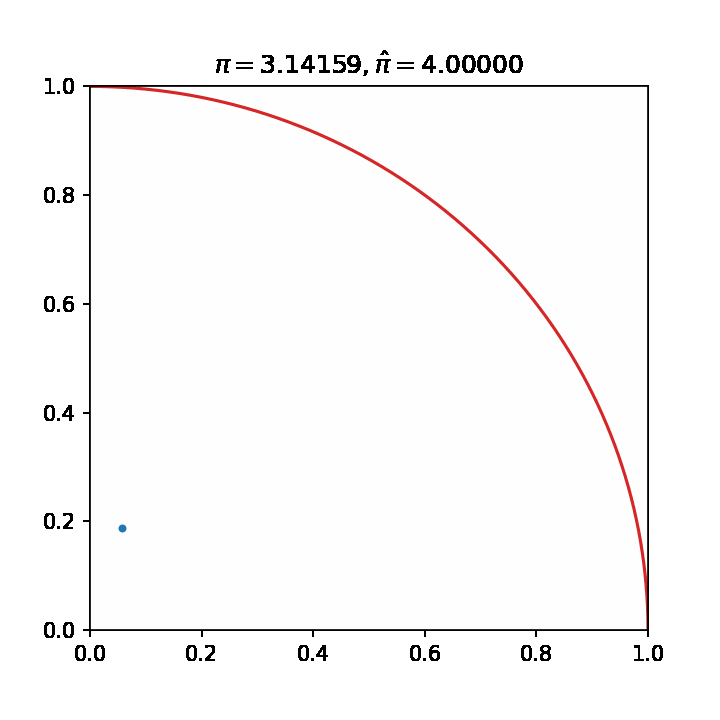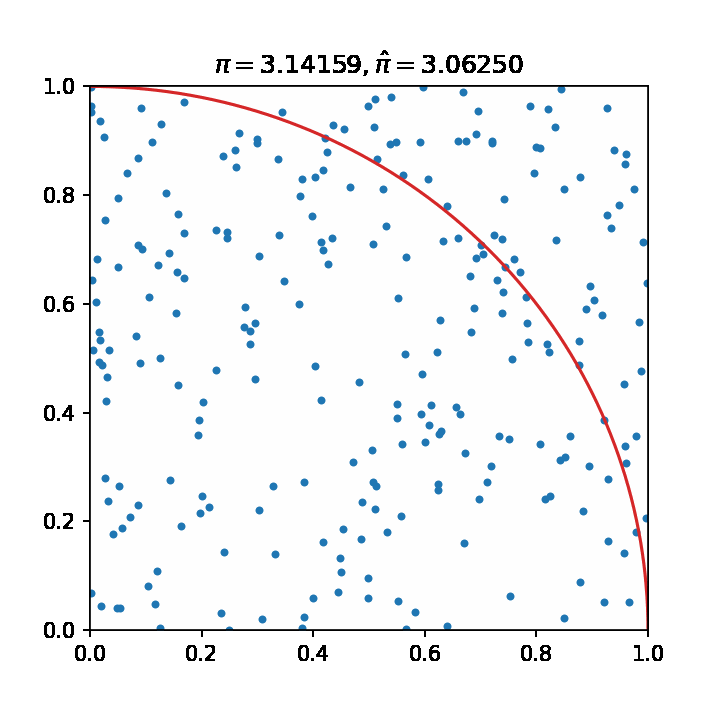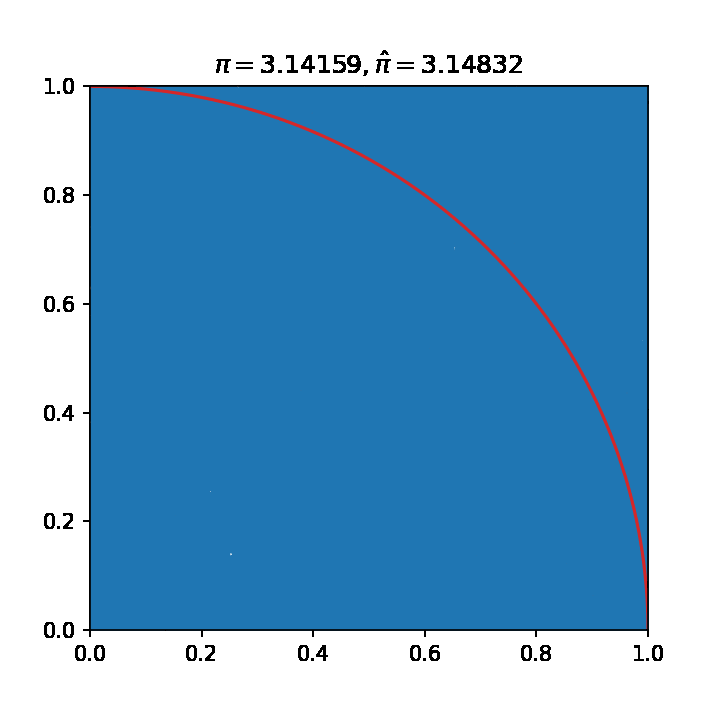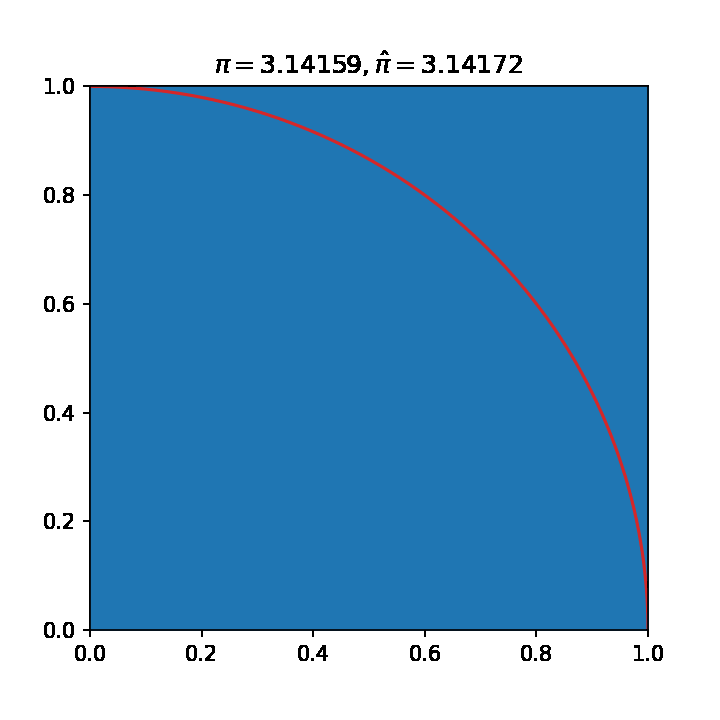
2. 数值积分
   

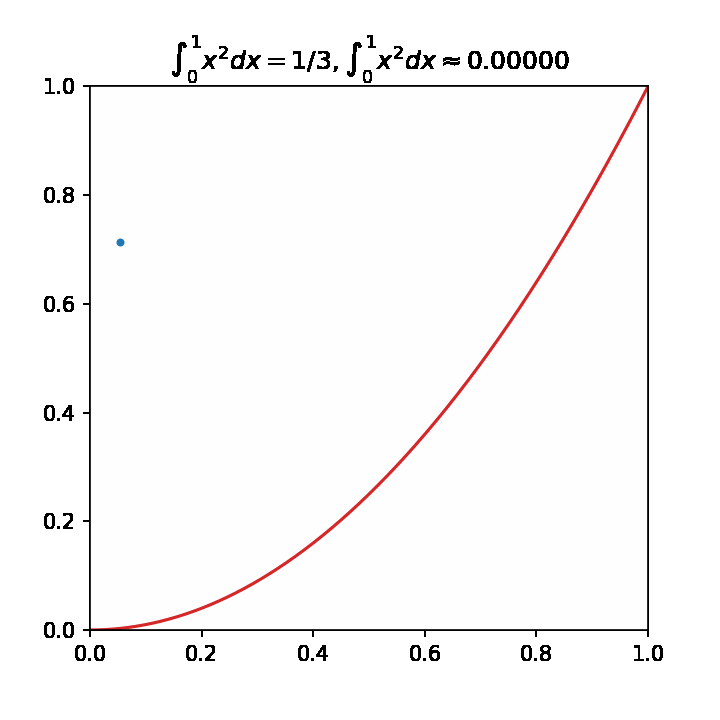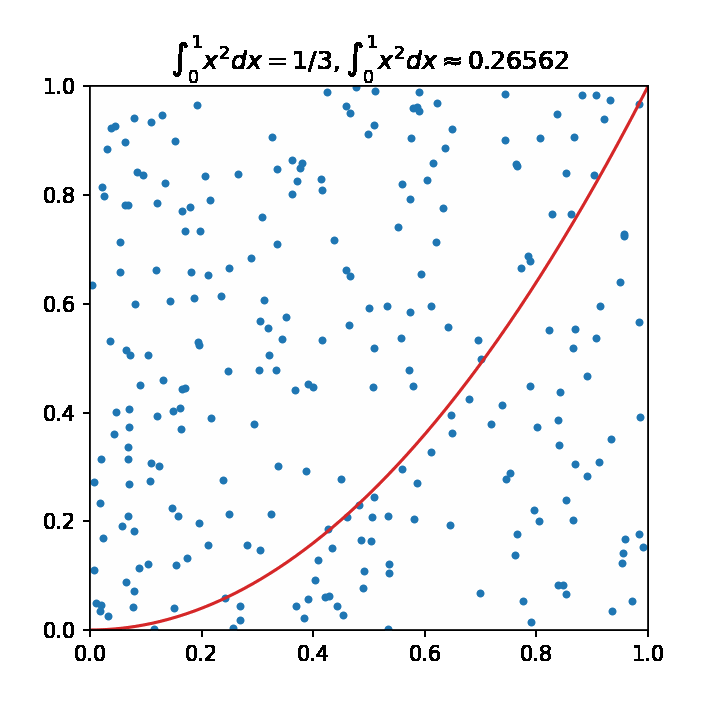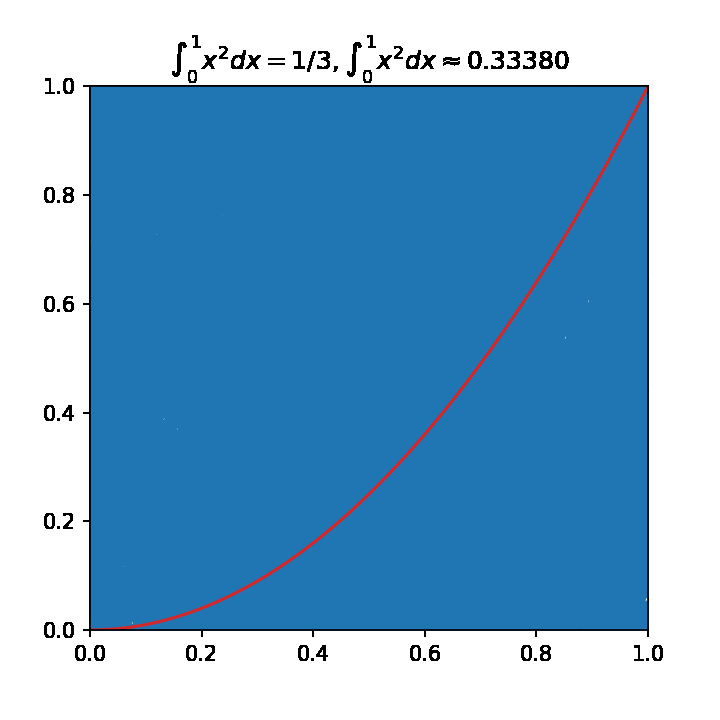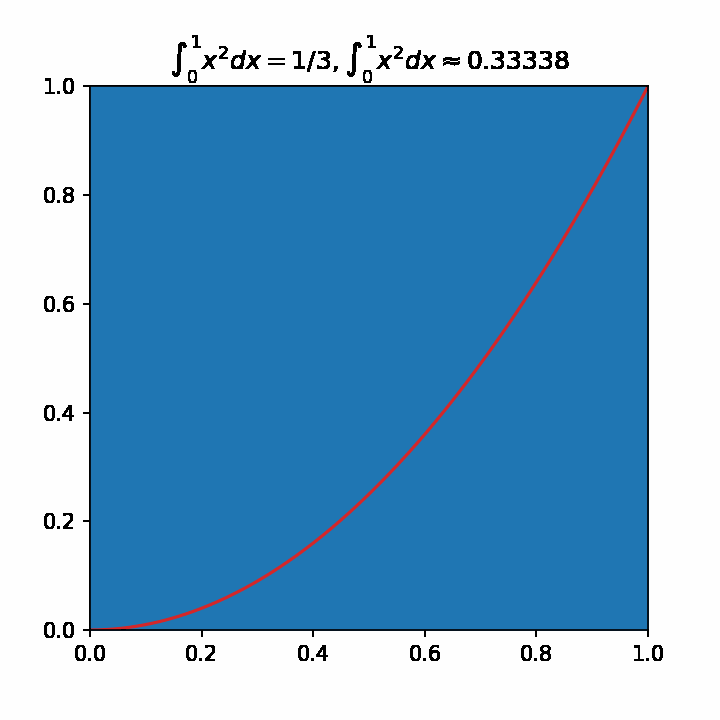
# 估算pi值
import matplotlib.pyplot as plt
%matplotlib inline
from matplotlib import animation
import numpy as np
fig,ax = plt.subplots(figsize=(4.8,4.8))
def estimate(data):
    return np.sum(data[:,0]**2+data[:,1]**2<=1)*4/data.shape[0]
def init():
    theta = np.linspace(0,np.pi/2,1000)
    circle_x = np.cos(theta)
    circle_y = np.sin(theta)
    ax.plot(circle_x,circle_y)
def animate(i):
    num = 2**i
    data = np.random.rand(num,2)
    ax.scatter(data[:,0],data[:,1],s=8,c="#d62728")
    ax.set_xlim([0,1])
    ax.set_ylim([0,1])
    ax.set_title("$\pi=3.14159,\hat{\pi}=%.5f$"%(estimate(data)))
ani = animation.FuncAnimation(fig=fig, func=animate, frames=23, init_func=init, interval=500, blit=False)
ani.save('pi.gif', dpi=150)